ATLAS empirical electron-muon test
December 27, 2021 at 2:59 pm 3 comments
A search for an unexpected asymmetry in the production of e+μ– and e–μ+ pairs in proton-proton collisions recorded by the ATLAS detector at √s = 13 TeV
This paper (arXiv:2112.08090), written by the ATLAS Collaboration, is original and interesting. The numbers of events with (e+μ–) and with (e–μ+) should be the same, according to the standard model (SM). So, if they are observed not to be the same, then new physics is at play. This specific idea was first proposed by Lester and Brunt: (arXiv:1612.02697) who focused on R-parity violating supersymmetric models. I will focus on the experimental analysis and skip the theoretical models.
The results are formulated in terms of a ratio, ρ, which is N(e+mu–) / N(e–mu+). Interestingly, the case ρ > 1 is easier to investigate than ρ < 1, and ATLAS does not derive results for the latter case. The problem is that non-prompt (a.k.a. “fake”) electrons are much more common than non-prompt muons, and W+are more common than W–, so W+ → μ+ and fake e– is more common than W+ → e+ and fake μ–. This bias is partially corrected for, and any new physics leading to ρ > 1 needs to be strong enough to overcome the remaining bias. The selection of electrons and muons is not unusual, and kinematically, they must have pT > 25 GeV and |η| < 2.47.
The bias (i.e., prevalence) of e–fakeμ+real over e+fakemu–real is handled by subtracting the appropriate number of background events (i.e., those with fake leptons) using a data-driven method. The contamination of the main signal region by fake leptons is small — only 2%. A very small effect due to the toroidal magnetic fields is corrected for by applying weights to events.
The event selection is rather simple, which is part of what makes this analysis appealing. An opposite-sign, electron-muon pair is required. In addition, ΣT, the sum of the transverse masses for the two leptons, must be at least 200 GeV. A subset of such events containing at least one jet (with pT > 20 GeV) is also analyzed. (Additional signal regions that are more model-inspired are defined, but I won’t be discussing them here.). The event yields are studied as functions of either MT2 or Hp, where Hp is just the scalar sum of the pT of the electron, muon, and leading jet.
Roughly 100k events are selected. The main contribution comes from top quark pair events — a process that is very well understood at the LHC. Diboson production is also important at the edge of the kinematic range. This nice plot shows the yield as a function of Hp.
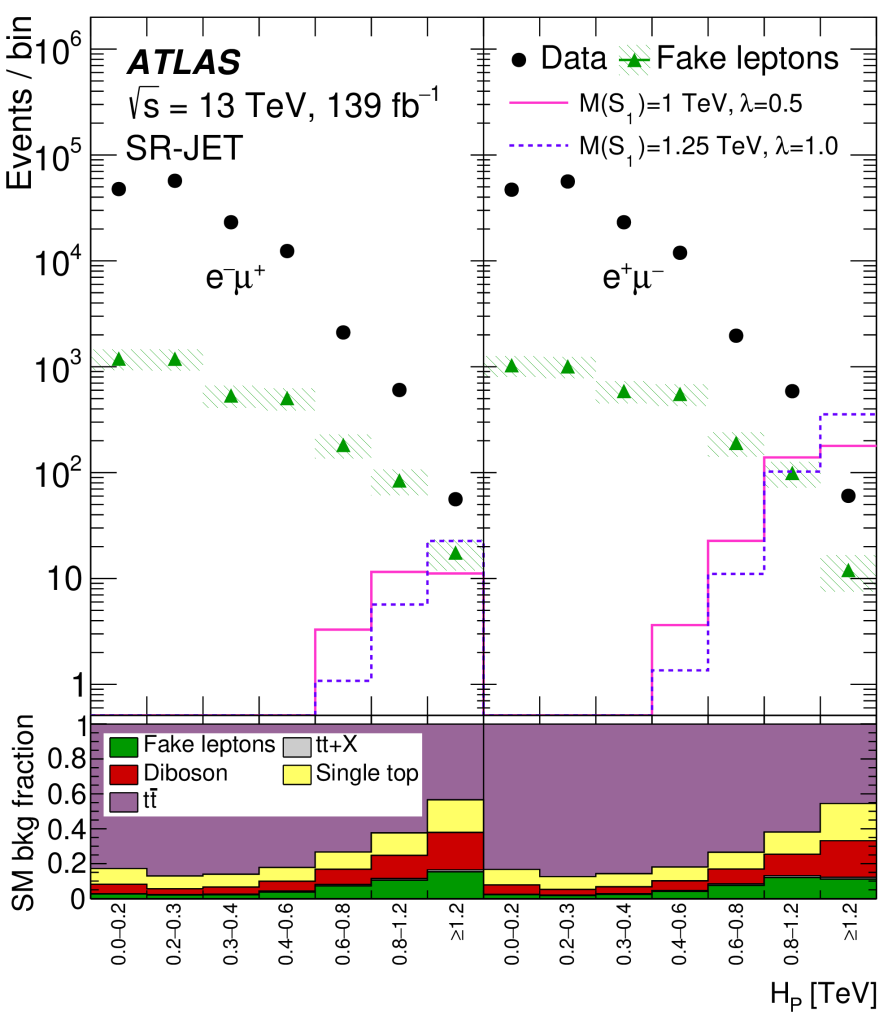
By eye there is no difference in yields for the two final states e–μ+ and e+μ–. A careful statistical treatment based on the likelihood for Poisson distributions in each bin leads to the following quantitative result: ρ = 0.987 ± 0.022 where I have neglected a small asymmetry in the error bar. Clearly, this measurement of ρ is consistent with unity and therefore with SM expectations. There is no evidence for ρ>1. Statistical p-values for all bins are quite reasonable — the largest deviation from unity is a downward fluctuation (3.1σ) in a single bin.
The authors go one to derive upper limits on the number of new physics signal events as a function of how those events are shared between the two final states (i.e., the fraction z that enter e–μ+). I find it striking that in some regions this analysis is sensitive to mere tens of events.
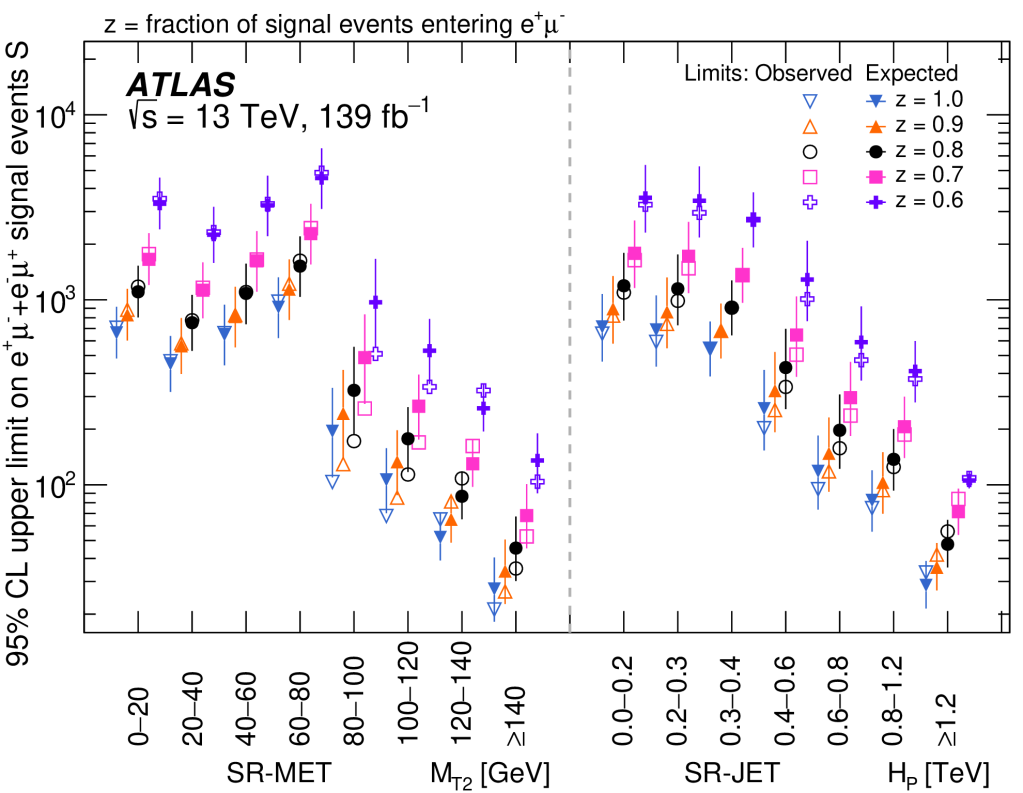
Of course, it would be wonderful to have a deviation from the SM expectation. Unfortunately, we do not have that here.
I like this analysis for its relatively inclusive nature and straight forward simplicity. There are many SM analyses which hope to see a deviation in a kinematic quantity such as jet pT or ST (which is similar to Hp here). What is relatively new is that this analysis looks at charge and flavor in the hopes of observing a telltale deviation. The two specific models considered in this paper — RPV-supersymmetry and leptoquarks — serve to demonstrate that new physics could lead to an observable deviation. I’m sure the authors will expand their final state and maybe tease out hints for new physics in a more sophisticated analysis.
https://arxiv.org/trackback/2112.08090
Entry filed under: Particle Physics.
3 Comments Add your own
Leave a comment
Trackback this post | Subscribe to the comments via RSS Feed
1. Wyrd Smythe | December 28, 2021 at 9:01 am
Wyrd Smythe | December 28, 2021 at 9:01 am
Good article, I appreciated it. I’ve been hoping ATLAS would turn up something. But once again, no new physics. That’s disappointing. (Maybe the g-2 experiment will turn up something.)
2. Michael Schmitt | December 28, 2021 at 9:16 am
Michael Schmitt | December 28, 2021 at 9:16 am
Thanks, I’m glad you like the article. Time will tell where signs of new physics turn up. It looks like some imagination will be required.
3. Wyrd Smythe | December 28, 2021 at 9:22 am
Wyrd Smythe | December 28, 2021 at 9:22 am
Indeed. The question I keep asking is whether we’re just a little off, there’s just some small point that will give us quantum gravity, or are we like Ptolemy and we’ve created a very clever, but completely incorrect, model? Do we need a correction or to wipe the slate clean and start over? That these tests keep confirming our model is almost disturbing somehow…